Seputar Pembahasan dan Penyelesaian Latihan Soal UN Matematika / Jurusan IPS tingkat SMA
Oleh Nirwan
 |
| MATEMATIKA |
Hai Sobat Nirwana 😁, selamat datang serta ketemu kembali di blog kesayangan kita dalam Seputar Catatan Unik & Akademik {Bang Nirwana}. Nah, jika sebelumnya Sobat Cerdas diajak bersama dalam ngebahas Seputar Kiat dan Persiapan Sebelum Menghadapi Ujian Nasional bagi Siswa/Siswi Tingkat SMA. Pada kesempatan berikutnya Sobat Cerdas bakal diajak kembali dalam mengasah skill akademis sebagai persiapan menghadapi UN di tingkat SMA. terutama, dikhususkan bagi Sobat SMA yang bakal menempuh UN di tahun ini ya..
UN yang semakin dekat terkadang menuntut para pelajar untuk semakin berjuang dalam menghadapi tantangan yang ada. Tak dipungkiri lagi, bakal banyak sekali persiapan yang harus dipikirkan atau dibikin secara matang untuk bisa sukses dalam menghadapi pelaksanaan UN yang dimaksud. Persiapan UN yang hanya mengandalkan niat serta target yang ingin dicapai masih belum cukup sebagai modal dan bekal yang akan dibawa pada hari Pelaksanaan Ujian. Tentu, bekal ilmu dan skill dalam menghadapi Soal-soal mata ujian juga amat diperhatikan. Persiapan dan penguasaan materi UN adalah kunci utama dalam menghadapi masa pelaksanaan Ujian Nasional. Nah, berikut blog Seputar Catatan Unik & Akademik {Bang Nirwana} bakal berbagi ilmu buat para Sobat sekalian, khususnya Sobat SMA yang bentar lagi bakal menghadapi masa Pelaksanaan UN di SMA tercinta. Sobat SMA, kami bakal mengajak kalian berlatih untuk menghadapi / menggali lebih dalam seputar gambaran atau bentuk Soal UN terutama Soal mengenai Mata Ujian Matematika bagi Sobat yang berjurusan Ilmu Pengetahuan Sosial (IPS). Untuk itu, banyaklah berlatih dan mendalami soal-soal berikut ya Sobat. moga bisa menjadi gambaran dan persiapan Sobat untuk mendukung penguasaan materi yang ada. Berikut Seputar Latihan serta pembahasan Soal UN Matematika / jurusan IPS tingkat SMA .
1. Misal x₁ dan x₂ adalah akar - akar persamaan kuadrat x² + 3x - 3 = 0 . Persamaan kuadrat yang akarnya 2x₁ - 1 dan 2x₂ - 1 adalah ...
Pembahasan & Penyelesaian :
Sebelum mengerjakan penyelesaian, perhatikan aturan persamaan kuadrat yang berlaku untuk bisa menyelesaikan /menjawab Soal diatas.
Setelah memahami aturan dasar diatas, perhatikan kembali bentuk persamaan kuadrat dari Soal Sebelumnya untuk menentukan aturan urutan sebagai berikut.
x² + 3x - 3 = 0
↓ ↓ ↓
a=1 b=3 c=3
Nah, Saatnya kita menyelesaikan langkah - langkah dari pertanyaan Soal diatas.
* ⋉ + B
* ⋉ . B
Jadi, Persamaan kuadrat yang akarnya
2x₁ - 1 dan 2x₂ - 1 pada pertanyaan Soal diatas adalah x² + 8x - 5 = 0
2. Himpunan penyelesaian pertidaksamaan dari 2x² + 5x - 3 <_ 0 adalah ...
Pembahasan & Penyelesaian :
Jadi, Himpunan penyelesaian dari pertidaksamaan 2x² + 5x - 3 <_ 0 adalah { x I -3 <_ x <_ , x ⋴ R }
3. Bentuk sederhana dari
adalah ...
Pembahasan & Penyelesaian :
Jadi, hasil Sederhana dari Soal bentuk pangkat diatas bisa dilihat pada gambar penyelesaian tersebut.
4. Diketahui x₁ dan x₂ adalah akar-akar persamaan kuadrat x² + 6x + 2 = 0. Nilai
x₁² + x₂² - 4 x₁ . x₂ adalah ...
Pembahasan & Penyelesaian :
Sama halnya Seperti pembahasan dan penyelesaian soal yang pertama, untuk menyelesaikan bentuk Soal persamaan kuadrat diatas terlebih dahulu kita menentukan aturan persamaan kuadrat yang berlaku sebagai berikut.
Berikut langkah - langkah dari proses penyelesaian Soal diatas. Perhatikan baik-baik .
Jadi, nilai x₁² + x₂² - 4 x₁ . x₂ adalah 24
5. Bentuk sederhana dari
adalah ...
Pembahasan & Penyelesaian :
Untuk menjawab Soal diatas, perhatikan langkah-langkah / proses penyelesaian dibawah ini.
Jadi, jawaban untuk Soal diatas adalah
6. Koordinat titik balik dari grafik fungsi y = x² - 2x + 4 adalah ...
Pembahasan & Penyelesaian :
Untuk mencari Koordinat titik balik, pergunakan rumus dasar yang biasa disebut dengan rumus ABC Sebagai berikut.
Setelah mempersiapkan rumus diatas, kita kembali menentukan urutan abjad = angka pada grafik fungsi berdasarkan Soal untuk menyesuaikan penggunaan rumus ABC nantinya.
grafik fungsi y = x² - 2x + 4
↓ ↓ ↓
a = 1 b = 2 c = 4
Tahap berikutnya adalah melanjutkan untuk mencari titik balik dari Soal yang dimaksud.
Jadi, titik balik dari grafik fungsi y = x² - 2x + 4 adalah (1,3)
7. Diketahui fungsi f = R - R dan fungsi g = R - R dirumuskan dengan f(x) = x - 1 dan g(x) = x² + 2x - 3. Fungsi (gof) adalah ...
Pembahasan & Penyelesaian :
Untuk mencari fungsi (gof) pada bentuk Soal diatas, Anda bisa memperhatikan penyelesaian berikut ini.
Jadi, fungsi (gof) yang kita temukan adalah x² - 4
8. Jika Matriks
maka, nilai dari x + 2y adalah ...
Pembahasan & Penyelesaian :
Substitusikan nilai x = 2 dan y = 6 pada x + 2y =
(2) + 2 (6) = 14.
Jadi, nilai x + 2y = 14
9. Diketahui matriks
Invers matriks x adalah ....
Pembahasan & Penyelesaian :
Untuk menyelesaikan matriks x menurut Soal diatas, perhatikan langkah penyelesaian berikut.
10. Dalam sebuah barisan aritmatika, suku ke-8 adalah 37 dan suku ke- 11 adalah 52. Jumlah Sepuluh suku pertama barisan tersebut adalah ...
Pembahasan & Penyelesaian :
Sebelum menyelesaikan atau mencari jumlah Sepuluh suku pertama dari barisan aritmatika diatas, hendaknya perhatikan rumus - rumus berikut.
Berikut langkah penyelesaiannya :
Jadi, jumlah Sepuluh suku pertama dari barisan aritmatika diatas adalah 245
11. Dik : f(x) = x + 1/2x - 3 dan f-1(x) menyatakan invers fungsi f(x) . Nilai f-1(1) adalah ...
Pembahasan & Penyelesaian :
Dalam mencari nilai f-1(1) berdasarkan bentuk Soal invers fungsi diatas, gunakan rumus berikut.
Langkah berikutnya, proses penyelesaian.
Jadi, Nilai f-1(1) adalah 4
12. Deret geometri tak hingga 6 + 3 + 3/2 + 3/4 + 3/8 + ... ?
Pembahasan & Penyelesaian :
13. ∫ (3x² - 4x + 5) dx = ...
Pembahasan & Penyelesaian :
Jadi, intgral tak tentu dari ∫ (3x² - 4x + 5) dx adalah x² - 2x³ + 5x + c
14. Turunan pertama dari
f(x) = (5x² - 4) ⁴ adalah ...
Pembahasan & Penyelesaian :
15. fungsi f(x) = x³ + 3x² - 9x + 10 naik pada interval ...
Pembahasan & Penyelesaian :
Untuk menyelesaikan Soal diatas, gunakan rumus turunan fungsi yang sudah pernah Anda pelajari.
Berikut penyelasaiannya.
Jadi, fungsi f(x) = x³ + 3x² - 9x + 10 naik pada interval x = -1 dan x = 3
16. ³∫ ( 6x² + 2x + 7 ) dx adalah ...
¹
Pembahasan & Penyelesaian :
Soal diatas merupakan bentuk mencari integral tertentu.
Untuk menyelesaikan Soal diatas , perhatikan penyelesaian dibawah ini.
17. Kombinisai dari ₅ C ₃ berikut adalah ...
Pembahasan & Penyelesaian :

Perhatikan rumus dari kombinasi diatas, gunakan rumus tersebut untuk mencari kombinasi ₅ C ₃ Berikut.
Proses Penyelesaian :
UN yang semakin dekat terkadang menuntut para pelajar untuk semakin berjuang dalam menghadapi tantangan yang ada. Tak dipungkiri lagi, bakal banyak sekali persiapan yang harus dipikirkan atau dibikin secara matang untuk bisa sukses dalam menghadapi pelaksanaan UN yang dimaksud. Persiapan UN yang hanya mengandalkan niat serta target yang ingin dicapai masih belum cukup sebagai modal dan bekal yang akan dibawa pada hari Pelaksanaan Ujian. Tentu, bekal ilmu dan skill dalam menghadapi Soal-soal mata ujian juga amat diperhatikan. Persiapan dan penguasaan materi UN adalah kunci utama dalam menghadapi masa pelaksanaan Ujian Nasional. Nah, berikut blog Seputar Catatan Unik & Akademik {Bang Nirwana} bakal berbagi ilmu buat para Sobat sekalian, khususnya Sobat SMA yang bentar lagi bakal menghadapi masa Pelaksanaan UN di SMA tercinta. Sobat SMA, kami bakal mengajak kalian berlatih untuk menghadapi / menggali lebih dalam seputar gambaran atau bentuk Soal UN terutama Soal mengenai Mata Ujian Matematika bagi Sobat yang berjurusan Ilmu Pengetahuan Sosial (IPS). Untuk itu, banyaklah berlatih dan mendalami soal-soal berikut ya Sobat. moga bisa menjadi gambaran dan persiapan Sobat untuk mendukung penguasaan materi yang ada. Berikut Seputar Latihan serta pembahasan Soal UN Matematika / jurusan IPS tingkat SMA .
1. Misal x₁ dan x₂ adalah akar - akar persamaan kuadrat x² + 3x - 3 = 0 . Persamaan kuadrat yang akarnya 2x₁ - 1 dan 2x₂ - 1 adalah ...
Pembahasan & Penyelesaian :
Sebelum mengerjakan penyelesaian, perhatikan aturan persamaan kuadrat yang berlaku untuk bisa menyelesaikan /menjawab Soal diatas.
Setelah memahami aturan dasar diatas, perhatikan kembali bentuk persamaan kuadrat dari Soal Sebelumnya untuk menentukan aturan urutan sebagai berikut.
x² + 3x - 3 = 0
↓ ↓ ↓
a=1 b=3 c=3
Nah, Saatnya kita menyelesaikan langkah - langkah dari pertanyaan Soal diatas.
* ⋉ + B
* ⋉ . B
Jadi, Persamaan kuadrat yang akarnya
2x₁ - 1 dan 2x₂ - 1 pada pertanyaan Soal diatas adalah x² + 8x - 5 = 0
2. Himpunan penyelesaian pertidaksamaan dari 2x² + 5x - 3 <_ 0 adalah ...
Pembahasan & Penyelesaian :
Jadi, Himpunan penyelesaian dari pertidaksamaan 2x² + 5x - 3 <_ 0 adalah { x I -3 <_ x <_ , x ⋴ R }
3. Bentuk sederhana dari
adalah ...
Pembahasan & Penyelesaian :
Jadi, hasil Sederhana dari Soal bentuk pangkat diatas bisa dilihat pada gambar penyelesaian tersebut.
4. Diketahui x₁ dan x₂ adalah akar-akar persamaan kuadrat x² + 6x + 2 = 0. Nilai
x₁² + x₂² - 4 x₁ . x₂ adalah ...
Pembahasan & Penyelesaian :
Sama halnya Seperti pembahasan dan penyelesaian soal yang pertama, untuk menyelesaikan bentuk Soal persamaan kuadrat diatas terlebih dahulu kita menentukan aturan persamaan kuadrat yang berlaku sebagai berikut.
Berikut langkah - langkah dari proses penyelesaian Soal diatas. Perhatikan baik-baik .
Jadi, nilai x₁² + x₂² - 4 x₁ . x₂ adalah 24
5. Bentuk sederhana dari
adalah ...
Pembahasan & Penyelesaian :
Untuk menjawab Soal diatas, perhatikan langkah-langkah / proses penyelesaian dibawah ini.
Jadi, jawaban untuk Soal diatas adalah
6. Koordinat titik balik dari grafik fungsi y = x² - 2x + 4 adalah ...
Pembahasan & Penyelesaian :
Untuk mencari Koordinat titik balik, pergunakan rumus dasar yang biasa disebut dengan rumus ABC Sebagai berikut.
Setelah mempersiapkan rumus diatas, kita kembali menentukan urutan abjad = angka pada grafik fungsi berdasarkan Soal untuk menyesuaikan penggunaan rumus ABC nantinya.
grafik fungsi y = x² - 2x + 4
↓ ↓ ↓
a = 1 b = 2 c = 4
Tahap berikutnya adalah melanjutkan untuk mencari titik balik dari Soal yang dimaksud.
Jadi, titik balik dari grafik fungsi y = x² - 2x + 4 adalah (1,3)
7. Diketahui fungsi f = R - R dan fungsi g = R - R dirumuskan dengan f(x) = x - 1 dan g(x) = x² + 2x - 3. Fungsi (gof) adalah ...
Pembahasan & Penyelesaian :
Untuk mencari fungsi (gof) pada bentuk Soal diatas, Anda bisa memperhatikan penyelesaian berikut ini.
Jadi, fungsi (gof) yang kita temukan adalah x² - 4
8. Jika Matriks
maka, nilai dari x + 2y adalah ...
Pembahasan & Penyelesaian :
Berikut langkah - langkah penyelesaiannya.
* mencari nilai x
* mencari nilai y
(2) + 2 (6) = 14.
Jadi, nilai x + 2y = 14
9. Diketahui matriks
Invers matriks x adalah ....
Pembahasan & Penyelesaian :
Untuk menyelesaikan matriks x menurut Soal diatas, perhatikan langkah penyelesaian berikut.
10. Dalam sebuah barisan aritmatika, suku ke-8 adalah 37 dan suku ke- 11 adalah 52. Jumlah Sepuluh suku pertama barisan tersebut adalah ...
Pembahasan & Penyelesaian :
Sebelum menyelesaikan atau mencari jumlah Sepuluh suku pertama dari barisan aritmatika diatas, hendaknya perhatikan rumus - rumus berikut.
Berikut langkah penyelesaiannya :
Jadi, jumlah Sepuluh suku pertama dari barisan aritmatika diatas adalah 245
11. Dik : f(x) = x + 1/2x - 3 dan f-1(x) menyatakan invers fungsi f(x) . Nilai f-1(1) adalah ...
Pembahasan & Penyelesaian :
Dalam mencari nilai f-1(1) berdasarkan bentuk Soal invers fungsi diatas, gunakan rumus berikut.
Langkah berikutnya, proses penyelesaian.
Jadi, Nilai f-1(1) adalah 4
12. Deret geometri tak hingga 6 + 3 + 3/2 + 3/4 + 3/8 + ... ?
Pembahasan & Penyelesaian :
13. ∫ (3x² - 4x + 5) dx = ...
Pembahasan & Penyelesaian :
Jadi, intgral tak tentu dari ∫ (3x² - 4x + 5) dx adalah x² - 2x³ + 5x + c
14. Turunan pertama dari
f(x) = (5x² - 4) ⁴ adalah ...
Pembahasan & Penyelesaian :
15. fungsi f(x) = x³ + 3x² - 9x + 10 naik pada interval ...
Pembahasan & Penyelesaian :
Untuk menyelesaikan Soal diatas, gunakan rumus turunan fungsi yang sudah pernah Anda pelajari.
Berikut penyelasaiannya.
Jadi, fungsi f(x) = x³ + 3x² - 9x + 10 naik pada interval x = -1 dan x = 3
16. ³∫ ( 6x² + 2x + 7 ) dx adalah ...
¹
Pembahasan & Penyelesaian :
Soal diatas merupakan bentuk mencari integral tertentu.
Untuk menyelesaikan Soal diatas , perhatikan penyelesaian dibawah ini.
17. Kombinisai dari ₅ C ₃ berikut adalah ...
Pembahasan & Penyelesaian :

Perhatikan rumus dari kombinasi diatas, gunakan rumus tersebut untuk mencari kombinasi ₅ C ₃ Berikut.
Proses Penyelesaian :
* Berikan respon Anda terhadap topik ini, Klik disini :
 Atau juga :
Atau juga :












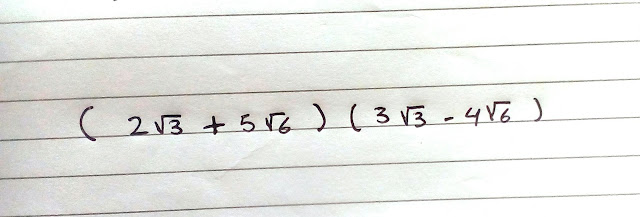































No comments:
Post a Comment
"Jadilah orang yang pertama kali berkomentar, kami siap mengapresiasi dan menerima masukan dari saudara. Terima Kasih"
Silahkan berkomentar secara bijak dan sopan dengan tidak saling menyudutkan / menyinggung pihak lain, menggunakan kata kasar maupun kotor, saling spam dan mengandung unsur SARA.
Anda juga dapat mengirim pesan melalui via Whatsapp dengan cara mengklik ikon Whatsapp yang telah tertera diatas jika ada sesuatu yang ingin ditanyakan.. 🤗