Seputar Pembahasan Soal dan Penyelesaian Fungsi Linear
Baca Juga : SEPUTAR PEMBAHASAN DAN PENYELESAIAN LATIHAN SOAL UN MATEMATIKA/JURUSAN IPS TINGKAT SMA
Untuk itulah, Seputar Catatan Unik & Akademik {Bang Nirwana} bakal berbagi kesempatan untuk membahas seputar materi terkait fungsi linear yang terkandung di dalam ilmu matematika. Untuk lebih jelasnya, mari kita perhatikan Pembahasan Seputar Soal dan Penyelesaian Fungsi Linear berikut ini.
Perhatikan gambar berikut.
- Pembahasan Soal fungsi linear melalui bentuk persamaan garis lurus.
Setelah Kedua titik sebelumnya telah ditentukan dengan Koordinat masing-masing (x1,y1) dan (x2,y2), selanjutnya sesuaikan (masukkan) kembali kedua titik yang telah ditentukan tersebut dengan menyesuaikan pada letak rumus diatas. Berikut langkah-langkah penyelesaian pada persamaan linear.
Nah, dari Penyelesaian tersebut, kita bisa melihat bahwa fungsi/persamaan linear yang didapat adalah y = 3 x - 22
itu artinya, kita telah menemukan persamaan linear yang dibentuk oleh titik A (4,-10) dan B (8,2) .
Langkah ketiga, Menentukan titik potong pada setiap Sumbu.
Untuk menentukan titik potong pada setiap sumbu, kita hanya perlu mensubstitusikan (mengganti) nilai 0 pada variabel x atau y pada persamaan yang kita dapat sebelumnya. Perhatikan penyelesaian berikut.
Langkah keempat, ditahap ini kita bakal membuat bentuk persamaan garis lurus / penentuan garis yang diambil dari persamaan linear yang telah didapat.
y = 3x - 22
Kita hanya menentukan posisi garis yang diambil dari nilai pada variabel x dan y yang didapat melalui penyelesaian titik potong sumbu.berikut hasil penggambaran dan penentuan garis yang dibentuk kedalam persamaan garis lurus.
- Pembahasan soal fungsi linear melalui bentuk tabel.
Pembahasan dan Penyelesaian:
Sejatinya, bentuk soal diatas tidaklah berbeda dengan penyelesaian pada persamaan linear sebelumnya. Hanya saja, penentuan titik yang bakal digunakan untuk membuat fungsi disajikan melalui bentuk sebuah tabel. Rumus yang digunakanpun masih sama,yaitu menggunakan rumus persamaan linear. Sedangkan untuk variabel x dan y sementara mengikuti bentuk dalam fungsi permintaan dan fungsi penawaran :
P = x dan q = y
Untuk penyelesaian soal diatas, langsung saja kita perhatikan langkah-langkah berikut.
Langkah pertama, seperti halnya pada pembahasan soal sebelumnya dari persamaan garis lurus. Langkah yang pertama kali dilakukan adalah menyesuaikan koordinat masing-masing (x1,y1) dan (x2,y2) pada titik yang terdapat didalam tabel.
untuk penyesuaian koodinat masing-masing (x1,y1) dan (x2,y2) pada titik melalui bentuk tabel, perhatikan gambar dibawah ini.
Telah jelas pada gambar tersebut bahwa di kolom1(p) baris 1 kiri terlihat angka 8 yang berkoordinat x1, sedangkan dikolom 2(q) baris 1 kanan terlihat angka 60 yang berkoordinat y1.jadi, titik A yang kita ambil pada tabel tersebut adalah (8,60).
Adapun untuk penentuan terhadap titik B pun sama halnya pada perlakuan titik A, pada kolom 1 dan 2 serta baris ke- 2 merupakan bagian titik B yang ditandai oleh warna biru laut.jadi, titik B yang diambil pada tabel adalah (10,50) .sehingga:
A (8,60) dan B (10,50)
Langkah Kedua, memasukkan kedua titik yang sudah ditentukan koordinatnya masing-masing kedalam rumus persamaan linear.
Dilanjutkan mencari/membuat fungsi permintaan (qd) Seperti yang diminta oleh soal. Untuk proses pada penyelesaian mencari fungsi permintaan (qd) berdasarkan soal yang dimaksud.Perhatikan langkah-langkah berikut.
Jadi, fungsi permintaan (qd) yang ditemukan adalah Qd = -5 p + 100.
- Pembahasan soal membuat fungsi permintaan (Qd) dan fungsi penawaran (Qs) menggunakan fungsi linear.
* Tentukan dan buatlah fungsi permintaan(Qd) dan fungsi penawaran(Qs) dari bentuk garis diatas !
* Carilah garis potong dari titik E !
Pembahasan dan Penyelesaian :
*Tentukan dan buatlah fungsi permintaan(Qd) dan fungsi penawaran(Qs) dari bentuk garis diatas!
Langkah pertama,
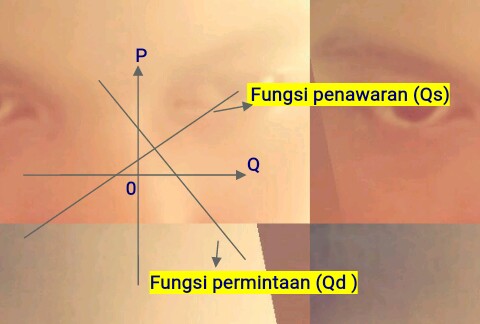
Untuk menjawab pertanyaan tersebut, kita terlebih dahulu menentukan posisi garis yang mengarah pada letak fungsi permintaan dan fungsi penawaran dalam bentuk soal. Seperti penjelasan diawal bahwa posisi garis untuk fungsi permintaan(Qd) berada pada arah serong kekiri, sedangkan posisi garis untuk fungsi penawaran(Qd) berada pada arah serong kekanan sebagai berikut.
~ Posisi garis yang menunjukkan letak fungsi permintaan (Qd) :
Dengan titik 6 (0,6) dan 3 (3,0)
~Posisi garis yang menunjukkan letak fungsi penawaran (Qs) :
Langkah kedua,
Menentukan Koordinat masing-masing (x1,y1) dan (x2,y2) dari titik yang ditemukan.
~Titik untuk fungsi permintaan (0,6) dan (3,0) :
x1 = 0 x2 = 3
y1 = 6 y2 = 0
~Titik untuk fungsi penawaran (0,3) dan (-6,0) :
x1 = 0 x2 = -6
y1 = 3 y2 = 0
Langkah ketiga,
Membuat fungsi permintaan ( Qd) dan fungsi penawaran (Qs).Untuk penyelesaian kedua fungsi tersebut perhatikan langkah-langkah berikut ini.
Gunakan Rumus Persamaan Linear yang sama.
~proses penyelesaian fungsi permintaan (Qd) :
Jadi, fungsi Permintaan (Qd) tersebut adalah Qd = -2 p + 6
~Proses penyelesaian fungsi penawaran (Qs) :
Jadi, fungsi penawaran (Qs) tersebut adalah Qs = 1/2 p + 3
*Carilah garis potong dari titik E !
Langkah pertama,
Siapkan kedua fungsi yang ditemukan ,
y = -2 x + 6 (dalam bentuk persamaan linear)
y = 1/2 x + 3 (dalam bentuk persamaan linear)
Langkah Kedua,
Selesaikan kedua fungsi diatas melalui metode Eliminasi dan Substitusi (Cara campuran) berikut ini.
~ Eliminasi
~ Substitusi
Jadi, garis potong dari titik E = (6/5 , 3 3/5)
* Berikan respon Anda terhadap topik ini, Klik disini :
http://www.strawpoll.me/17597367/r
 Atau juga :
Atau juga :



































numpang share ya min ^^
ReplyDeletebuat kamu yang lagi bosan dan ingin mengisi waktu luang dengan menambah penghasilan yuk gabung di di situs kami www.fanspoker.com
kesempatan menang lebih besar yakin ngak nyesel deh ^^,di tunggu ya.
|| bbm : 55F97BD0 || WA : +855964283802 || LINE : +855964283802 ||